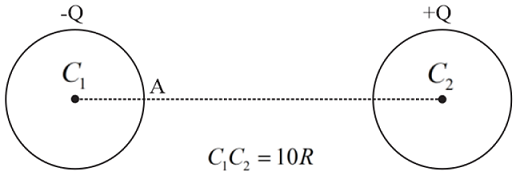Question

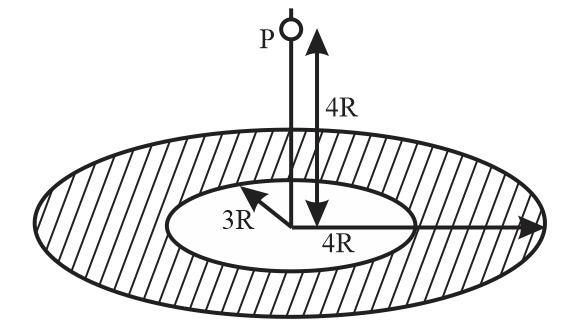
A thin uniform annular disc of mass $M$ , has an outer radius of $4R$ and an inner radius of $3R$ as shown in the figure. The work required to take a unit mass from point $P$ on its axis to infinity is

• A. $\frac{2 \textit{GM}}{7 \textit{R}} \left(4 \sqrt{2} - 5\right)$
• B. $- \frac{2 G M}{7 R} \left(\right. 4 \sqrt{2} - 5 \left.\right)$
• C. $\frac{\text{GM}}{4 \text{R}}$
• D. $\frac{2 \text{GM}}{5 \text{R}} \left(\sqrt{2} - 1\right)$

Answer 1

Answer: (A)

$\textit{W} = \Delta \textit{U} = \textit{U}_{\textit{f}} - \textit{U}_{\textit{i}} = \textit{U}_{\infty } - \textit{U}_{\textit{P}}$
$=-U_P=-m V_P=-V_P \quad($ as $m=1)$
Upon integration, potential at point P will be obtained as given below
Let dM be the mass of small ring as shown
$\textit{dM} = \frac{\textit{M}}{\pi \left(4 \textit{R}\right)^{2} - \pi \left(3 \textit{R}\right)^{2}} \left(2 \pi \textit{r}\right) \textit{dr} = \frac{2 \textit{Mr} \textit{dr}}{7 \left(\textit{R}\right)^{2}}$
$\textit{dV}_{\text{P}} = - \frac{\textit{G} \textit{d} \textit{M}}{\sqrt{1 6 \textit{R}^{2} + \text{r}^{2}}}$

$= - \frac{2 \textit{GM}}{7 \textit{R}^{2}} \displaystyle \int _{3 \textit{R}}^{4 \textit{R}} \frac{\textit{r}}{\sqrt{1 6 \textit{R}^{2} + \textit{r}^{2}}} \textit{dr}$
$= - \frac{2 G M}{7 R} \left(\right. 4 \sqrt{2} - 5 \left.\right)$
$\therefore \textit{W} = + \frac{2 \textit{GM}}{7 \textit{R}} \left(4 \sqrt{2} - 5\right)$ $$