Question

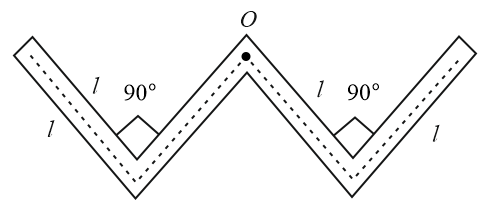
A thin rod of length $4l$ , mass $4m$ is bent at three points as shown in the figure. What is the moment of inertia of the rod about the axis passing through point $O$ and perpendicular to the plane of the paper?

• A. $\frac{m l^{2}}{12}$
• B. $\frac{10 m l^{2}}{3}$
• C. $\frac{2 m l^{2}}{12}$
• D. $\frac{m l^{2}}{24}$

Answer 1

Answer: (B)

Let's suppose points are $A, B, C, D$
Total moment of inertia about an axis passing through point $O$ and perpendicular to the plane of paper is
$I_{n e t}=I_{A B}+I_{B O}+I_{O C}+I_{C D} \ldots(i)$
Let's suppose points $P, Q, R, S$ are the middle points of all rods respectively.
Now using parallel axis theorem
$I_{B O}=I_{O C}=\frac{m l^2}{12}+(m)\left(\frac{l}{2}\right)^2 $
$I_{B O}=I_{O C}=\frac{m l^2}{3}$
Now,
Distance $P O=?$


Using Pythagoras theorem,
$x=P O=\sqrt{l^2+\frac{l^2}{4}}=\frac{\sqrt{5} l}{2}$
Now,$I_{A B}=I_{C D}=\frac{m l^2}{12}+m\left(\frac{\sqrt{5} l}{2}\right)^2$
(Using parallel axis theorem)
So, $I_{A B}=I_{C D}=\frac{4}{3} m l^2$
Now putting values in eq. (i)
$I_{n e t}=\frac{m l^2}{3}+\frac{m l^2}{3}+\frac{4}{3} m l^2+\frac{4}{3} m l^2 $
$I_{n e t}=\frac{10}{3} m l^2$
So option (2) is correct