Question

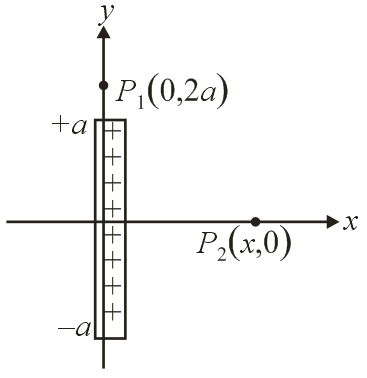
A thin rod of length $2a$ is placed along $y$ -axis in the $x-y$ plane. The rod carries a charge density $\lambda $ as shown in figure. If point $P_{1}$ is located at $\left(0 , 2 a\right)$ and $P_{2}$ at $\left(x , 0\right),$ then find $\left(\frac{x}{a}\right)^{2}$ if potential at $P_{1}$ and $P_{2}$ are equal.

Answer 1

$v_{1}=k\displaystyle \int _{- a}^{a}\frac{\lambda d y}{\left(2 a - y\right)}=k\lambda ln3$
$v_{2}=k\displaystyle \int _{- a}^{+ a}\frac{\lambda d y}{\sqrt{y^{2} + x^{2}}}$
$=2k\lambda ln\left(\frac{a + \sqrt{a^{2} + x^{2}}}{x}\right)$
$\because v_{1}=v_{2}$
$k\lambda ln3=2k\lambda ln\left(\frac{a + \sqrt{a^{2} + x^{2}}}{x}\right)$
$\sqrt{3}x=a+\sqrt{a^{2} + x^{2}}$
$\frac{x}{a}=\sqrt{3}=1.732$
$1.73$