Question

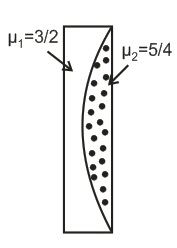
A thin plano-convex lens fits exactly into a plano-concave lens with their plane surface parallel to each other as shown in the figure. The radius of curvature of the curved surface $R=30 cm$ . The lens is made of a different material having refractive index $\mu_{1}=\frac{3}{2}$ and $\mu_{2}=\frac{5}{4}$ as shown in the figure. If the plane surface of the plano-convex lens is silvered, then calculate the equivalent focal length of this system in $cm$.

Answer 1

(i) $P_{e q}=2 P_{\ell 1}+2 P_{\ell 2}+P_{m} \ldots(1)$
For plano-convex lens: $\frac{1}{( f )_{t}}=\left(\frac{3}{2}-1\right)\left(\frac{1}{\infty}-\frac{1}{30}\right)$
$f _{\ell 1}=-60\, cm$
$\Rightarrow P _{\ell 1}=\frac{100}{ f _{\ell 1}}$
$\Rightarrow P _{\ell 1}=-\frac{5}{3} D$
For plano-convex lens: $\frac{1}{( f )_{P}}=\left(\frac{5}{4}-1\right)\left(\frac{1}{30}-\frac{1}{\infty}\right)$
$\Rightarrow \frac{1}{ f _{C 2}}=\frac{1}{120}$
$f _{\ell 2}=120 cm \Rightarrow P _{\ell 2}=\frac{100}{ f _{\ell 2}}$
$\Rightarrow P _{\ell 2}=\frac{5}{6} D$
For plane mirror: $P _{ m }=0$ sincef $_{ m }=\infty$
$\Rightarrow P _{ eq }=2 P _{\ell 1}+2 P _{\ell 2}+ P _{ m }$
$P _{\text {eq }}=-\frac{10}{3}+\frac{10}{6}+0$
$\Rightarrow P _{\text {eq }}=-\frac{10}{6} D$
$\because P_{\text {eq }}=-\frac{1}{F_{\text {eq }}}$
$\Rightarrow F_{\text {eq }}=60\, cm$