Question

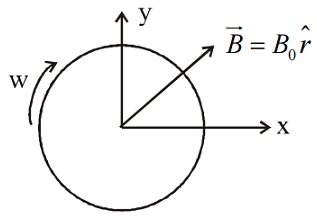
A thin non conducting disc of mass M = 2kg, charge $Q=2\times 10^{- 2} \, C$ and radius $R=\frac{1}{6}m$ is placed on a frictionless horizontal plane with its centre at the origin of the coordinate system. A non uniform, radial magnetic field $\overset{ \rightarrow }{B}=B_{0} \, \hat{r}$ exists in space, where $B_{0}=10T$ and $\hat{r}$ is a unit vector in the radially outward direction. The disc is set in motion with an angular velocity $\omega =x\times 10^{2}$ rad/sec, about an axis passing through its centre and perpendicular to its plane, as shown in the figure. At what value of x, the disc will lift off from the surface.

Answer 1

The force an any small part of the disc is in the vertically upward direction
$dF=\left(\frac{Q}{\pi R^{2}} 2 \pi r \, d r\right)\omega r \, B_{0}$
$dF=\frac{2 Q \omega B_{0}}{R^{2}} \, r^{2} \, dr$


$F=\frac{2}{3}Q\omega B_{0}R=Mg \, $
$\Rightarrow \omega =\frac{3 M g}{2 Q B_{0} R}=\frac{3 \times 2 \times 10}{2 \times 2 \times 10^{- 2} \times 10 \times \frac{1}{6}}=9\times 10^{2} \, r a d / s$