Q.
A thin glass rod is bent into a semi circle of radius $r$. A charge $+q$ is uniformly distributed along the upper half and a charge $-q$ is uniformly distributed along the lower half, as shown in the figure. The magnitude and direction of the electric field $\vec{E}$ produced at $P$, the centre of the circle, will be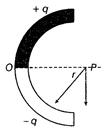
AMUAMU 2013Electric Charges and Fields
Solution:
Take $PO$ as the $x$-axis and $PA$ as the $y$-axis. Consider two elements $EF$ and $E ^{\prime} F ^{\prime}$ of width $d \theta$ at angular distance $\theta$ above and below PO, respectively.
The magnitude of the field at $P$ due to either element is
$dE =\frac{1}{4 \pi \varepsilon_{0}} \frac{ rd \theta \times Q /(\pi r / 2)}{ r ^{2}}=\frac{ Q }{2 \pi^{2} \varepsilon_{0} r ^{2}} d \theta$
Resolving the fields, we find that the components along PO sum up to zero, and hence the resultant field is along PA.
Therefore, field at $P$ due to pair of elements is $2 E \sin \theta$
$ E =\int\limits_{0}^{\pi / 2} 2 E \sin \theta $
$=2 \int\limits_{0}^{\pi / 2} \frac{ Q }{2 \pi^{2} \varepsilon_{0} r ^{2}} \sin \theta d \theta=\frac{ Q }{\pi^{2} \varepsilon_{0} r ^{2}}$
