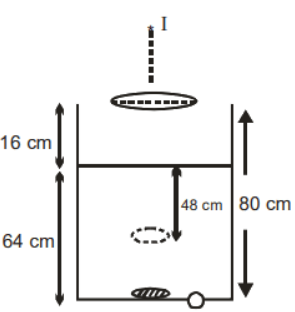
Question

A thin convex lens is placed just above an empty vessel of depth $80\, cm$. The image of a coin kept at the bottom of the vessel is thus formed $20 \,cm$ above the lens. If now water is poured in the vessel up to a height of $64\, cm$, what will be the approximate new position of the image. Assume that refractive index of water is $4 / 3$.

• A. 21.33 cm above the lens
• B. 6.67 cm below the lens
• C. 33.67 cm above the lens
• D. 24 cm above the lens

Answer 1

Answer: (A)

$u =-80\, cm $
$v =+20 \,cm$
$\frac{1}{f}=\frac{1}{v}-\frac{1}{u}=\frac{1}{20}+\frac{1}{80}=\frac{5}{80}$
$f=16 \,cm$
$u'=16+\frac{64 \times 3}{4}=64 \,cm$
$\frac{1}{16}=\frac{1}{v}+\frac{1}{64}$
$\therefore \frac{1}{v}=\frac{1}{16}-\frac{1}{64}=\frac{3}{64}$
$v =21.33$ above the lens