Question

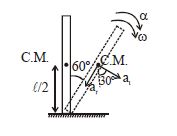
A thin and uniform rod of mass M and length L is held vertical on a floor with large friction. The rod is released from rest so that it falls by rotating about its contact-point with the floor without slipping. Which of the following statement(s) is/are correct, when the rod makes an angle 60$^{\circ}$ with vertical ?
[g is the acceleration due to gravity]

• A. The radial acceleration of the rod's center of mass will be $\frac{3 g}{4}$
• B. The angular acceleration of the rod will be $\frac{2 g}{L}$
• C. The angular speed of the rod will be $\sqrt{\frac{3g}{2L}}$
• D. The normal reaction force from the floor on the rod will be $\frac{M g}{16}$

Answer 1

Answer: (A), (C), (D)

We can treat contact point as hinged.
Applying work energy theorem
$W_{g} = \Delta KE.$

$mg \frac{\ell}{4} = \frac{1}{2}\left(\frac{m\ell^{2}}{3}\right)\omega^{2}$

$\omega = \sqrt{\frac{3g}{2\ell}}$

radial acceleration of C.M. of rod $= \left(\frac{\ell}{2}\right)\omega^{2} = \frac{3g}{4}$

Using $\tau = I \alpha$ about contact point

$\frac{mg\ell}{2}sin\,60^{\circ} = \frac{m\ell^{2}}{3}\alpha$

$\Rightarrow \,\alpha = \frac{3\sqrt{3}}{4\ell}g$

Net vertical acceleration of C.M. of rod

$a_{v} = a_{r} \,cos\,60^{\circ} + a_{t} \,cos\,30^{\circ}$

$= \left(\frac{3g}{4}\right) \left(\frac{1}{2}\right) + \left(\alpha \frac{\ell}{2}\right)cos\,30^{\circ}$

$= \frac{3g}{8}+\frac{3\sqrt{3g}}{4\ell}\left(\frac{\ell}{2}\right)\left(\frac{\sqrt{3}}{2}\right)$

$= \frac{3g}{g}+\frac{9g}{16} = \frac{15}{16}g$

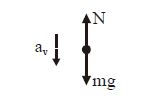
Applying $F_{net}$ = ma in vertical direction on rod as system

$mg - N = ma_{v} = m \left(\frac{15}{16}g\right)$

$\Rightarrow \,N = \frac{mg}{16}$