Question

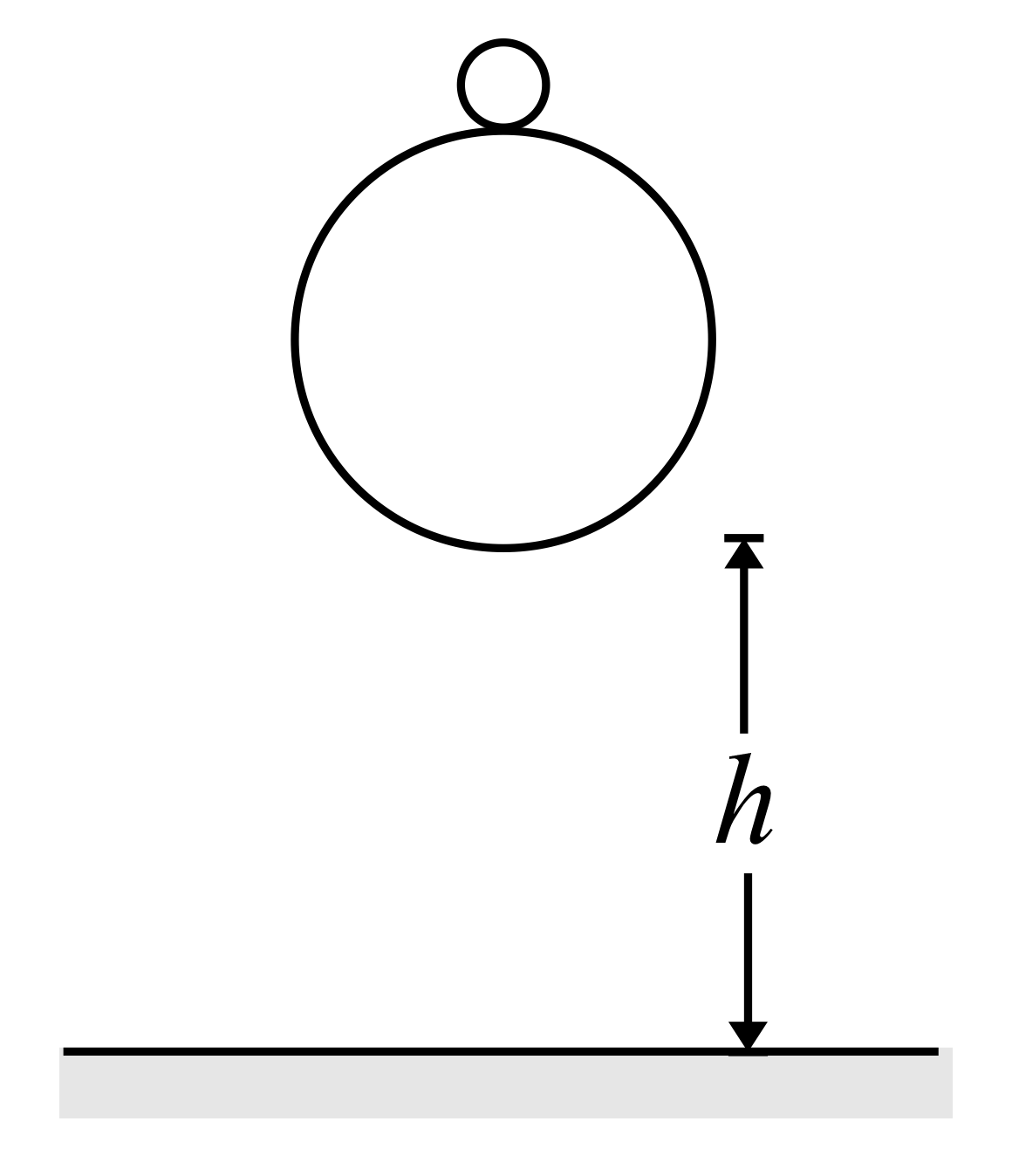
A tennis ball with (small) mass $m_{2}$ , sits on the top of a basketball with (large) mass $m_{1}$ . The bottom of the basketball is at a height $h$ above the ground and the bottom of the tennis ball is at a height $\left(\right.h+d\left.\right)$ above the ground. The balls are dropped from rest. Here all collisions are elastic and $m_{1}>>m_{2}$ . The height from the point of collision up to which the tennis ball bounce is

• A. $h$
• B. $2h$
• C. $3h$
• D. $9h$

Answer 1

Answer: (D)

Just before the collision, the velocity of the basketball in the downward direction is $\sqrt{2 g h}$ and just after the collision its velocity reverses its direction
So just after the collision, the downward moving tennis ball collides with upward moving basketball. The velocity of the tennis ball after this collision is
$v=-\left(- 2 \sqrt{2 g h}\right)+\sqrt{2 g h}\Rightarrow v=3\sqrt{2 g h}$
The height up to which the tennis ball will bounce is
$h^{'}=\frac{\left(3 \sqrt{2 g h}\right)^{2}}{2 g}\Rightarrow h^{'}=9h$