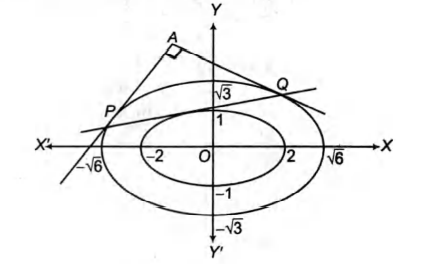
Question

A tangent to the ellipse $ x^2 + 4y^2 = 4 $ meets the ellipse $ x^2 + 2y^2 = 6 $ at $P$ and $Q$. Prove that the tangents at $P$ and $Q$ of the ellipse $x^2 + 2y^2 = 6 $ are at right angles

Answer 1

Given, $x^{2}+4 y^{2}=4$ or $\frac{x^{2}}{4}+\frac{y^{2}}{1}=1 \ldots$ (i)
Equation of any tangent to the ellipse on (i) can be written as
$\frac{x}{2} \cos \theta+y \sin \theta=1 ...$ (ii)
Equation of second ellipse is

$ x^{2}+2 y^{2} =6$
$\Rightarrow \frac{x^{2}}{6}+\frac{y^{2}}{3} =1 .... $(iii)
Suppose the tangents at $P$ and $Q$ meets at $A(h, k)$. Equation of the chord of contact of the tangents through $A(h, k)$ is
$\frac{h x}{6}+\frac{k y}{3}=1 ....$ (iv)
But Eqs. (iv) and (ii) represent the same straight line, so comparing Eqs. (iv) and (ii), we get
$\frac{h / 6}{\cos \theta / 2}=\frac{k / 3}{\sin \theta}=\frac{1}{1}$
$\Rightarrow h=3 \cos \theta$ and $k=3 \sin \theta$
Therefore, coordinates of $A$ are $(3 \cos \theta, 3 \sin \theta)$.
Now, the joint equation of the tangents at $A$ is given by $T^{2}=S S_{1}$,
i.e. $\left(\frac{h x}{6}+\frac{k y}{3}-1\right)^{2}=\left(\frac{x^{2}}{6}+\frac{y^{2}}{3}-1\right)\left(\frac{h^{2}}{6}+\frac{k^{2}}{3}-1\right) \ldots$ (v)
In Eq. (v), coefficient of $x^{2}=\frac{h^{2}}{36}-\frac{1}{6}\left(\frac{h^{2}}{6}+\frac{k^{2}}{3}-1\right)$
$=\frac{h^{2}}{36}-\frac{h^{2}}{36}-\frac{k^{2}}{18}+\frac{1}{6}=\frac{1}{6}-\frac{k^{2}}{18}$
and coefficient of $y^{2}=\frac{k^{2}}{9}-\frac{1}{3}\left(\frac{h^{2}}{6}+\frac{k^{2}}{3}-1\right)$
$=\frac{k^{2}}{9}-\frac{h^{2}}{18}-\frac{k^{2}}{9}+\frac{1}{3}=-\frac{h^{2}}{18}+\frac{1}{3}$
Again, coefficient of $x^{2}+$ coefficient of $y^{2}$
$=-\frac{1}{18}\left(h^{2}+k^{2}\right)+\frac{1}{6}+\frac{1}{3} $
$=-\frac{1}{18}\left(9 \cos ^{2} \theta+9 \sin ^{2} \theta\right)+\frac{1}{2}=-\frac{9}{18}+\frac{1}{2}=0$
which shows that two lines represent by Eq. (v) are at right angles to each other.