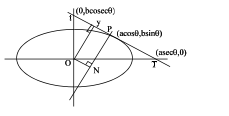
Question

A tangent is drawn to the curve, $\frac{x^2}{16}+\frac{y^2}{9}=1$ at the point $P$ meeting the co-ordinate axis in $T$ and $t$ If OY is the perpendicular from the origin on the tangent then find the value of the product ( $Tt$ ) (PY).

Answer 1

Tangent at $P: \frac{x \cos \theta}{a}+\frac{y \sin \theta}{b}=1$
T: $(a \sec \theta, 0), t:(0, b \operatorname{cosec} \theta)$
hence $Tt =\sqrt{ a ^2 \sec ^2 \theta+ b ^2 \operatorname{cosec}^2 \theta}$
To find $Py$, we draw normal at $P$.
now $ON = Py$
Hence Normal at $P \frac{ ax }{\cos \theta}-\frac{ by }{\sin \theta}= a ^2- b ^2$
$ON : \frac{ a ^2- b ^2}{\sqrt{ a ^2 \sec ^2 \theta+ b ^2 \operatorname{cosec}^2 \theta}}= Py$
Hence Py. $Tt = a ^2- b ^2$