Q.
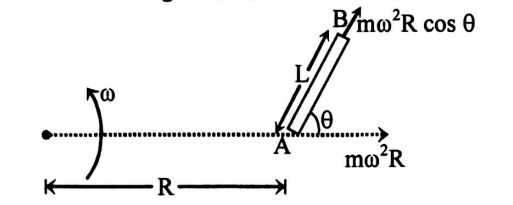
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity $\omega$ in a circular path of radius $R$. A smooth groove $A B$ of length $L < < R$ is made on the surface of the table. The groove makes an angle $60^{\circ}$ with the radius $OA$ of the circle in which the cabin rotates. A small particle is kept at the point $A$ in the groove and is released to move along $A B$. The time taken by the particle to reach the point $B$ is a $\sqrt{\frac{L}{\omega^{2} R}}$. Determine a.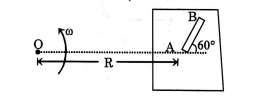
Laws of Motion
Solution: