Question

A student measures pressure of a gas in a container using a mercury manometer and she also measures atmospheric pressure using a mercury barometer. She gave following representation

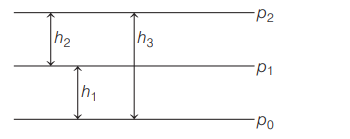
If $p_{1}=$ atmospheric pressure,
and $p_{2}=$ absolute pressure, then

• A. gauge pressure $=h_{1}+h_{2}$
• B. gauge pressure $=h_{3}-h_{1}$
• C. gauge pressure $=h_{3}$
• D. absolute pressure $=h_{1}$

Answer 1

Answer: (B)

As we know that, if $p_{1}$ represents the atmospheric pressure, then absolute pressure $p^{\prime}=p_{1}+\rho g h$ and gauge pressure, $p^{\prime \prime}=p^{\prime}-p_{1}=\rho g h$
From the given figure, we can write, $p_{1}=\rho g h_{1}$
$\Rightarrow p^{\prime}=p_{2}=\rho g h_{1}+\rho g h_{2}=\rho g\left(h_{1}+h_{2}\right)=\rho g h_{3}$
Similarly, $p^{\prime \prime}=p_{2}-p_{1}=\rho g h_{3}-\rho g h_{1}$
$=\rho g\left(h_{3}-h_{1}\right)=\rho g h_{2}$
$\therefore$ In terms of height, we can write,
Absolute pressure $=h_{3}=h_{1}+h_{2}$
Gauge pressure $=h_{2}=h_{3}-h_{1}$