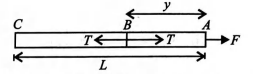
Question

A string of length $L$ and mass $M$ is lying on a horizontal table. A force $F$ is applied at one of its ends. Tension in the string at a distance $y$ from the end at which the force applied is

• A. zero
• B. $F$
• C. $\frac{F(L-y)}{L}$
• D. $\frac{F(L-y)}{M}$

Answer 1

Answer: (C)

Acceleration of the rope, $a=\frac{F}{M} \,\,\, \ldots (i)$

Now, considering the motion of the part $A B$ of the rope
[which has mass $(M / L) y$ and acceleration given by eq. $(i)$]
assuming that tension at $B$ is $T$.
$F-T=\left(\frac{M}{L} y\right) \times a \quad \text { or } \quad F-T=\frac{M}{L} y \times \frac{F}{M}=\frac{F y}{L} $
$ or \,\,\,\, T=F-F \frac{y}{L}=F\left(1-\frac{y}{L}\right)=\frac{F(L-y)}{L}$