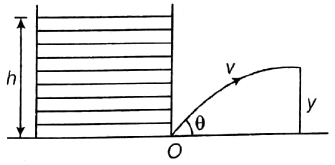
Q.
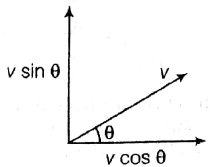
A stream of non-viscous liquid emerges from a very short outlet tube at the base of a large open tank, in which the depth of liquid is $h$ . The tube is at a fixed angle $\theta $ to the ground as shown in the figure. The maximum height of the stream $y$ is
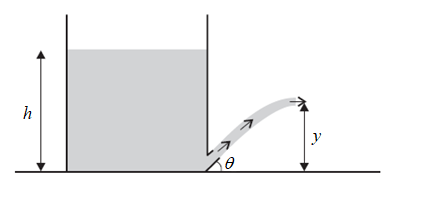
NTA AbhyasNTA Abhyas 2020
Solution: