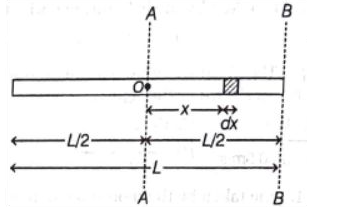
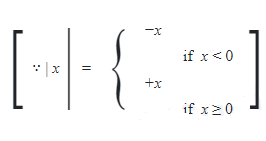Question

A straight rod of length $L$ is made of a material having mass per unit length $m(x)=\lambda |x|$, where $x$ is measured from the centre of rod. The moment of inertia about an axis perpendicular to the rod and passing through one end of the rod will be, $L=1\, m$ and $\lambda=16\, kg / m ^{2}$

• A. $\frac{32}{3} kg - m ^{2}$
• B. $40 \,kg - m ^{2}$
• C. $\frac{36}{5} kg - m ^{2}$
• D. $246\, kg - m ^{2}$

Answer 1

Answer: (A)

Mass per unit length,
$\frac{d M}{d x}=\lambda |x|$
$\Rightarrow d M=\lambda |x| d x$

Moment of inertia about axis $A A$
$I_{A A}=\int x^{2} d M$
Put the value of $d M$
$I_{A A}=\int\limits_{-L / 2}^{+L / 2} x^{2} \times \lambda |x| d x=\int\limits_{-L / 2}^{+L / 2} x^{2} \times 16|x| d x$
$\left[\because \lambda=16\, kg / m ^{2} \text { (given) }\right]$
$=16 \int\limits_{-L / 2}^{+L / 2} x^{2}|x| d x$
$=16\left[\int\limits_{-L / 2}^{0} x^{2}(-x) d x+\int\limits_{0}^{+L / 2} x^{2}(+x) d x\right]$

So, $I_{A A}=16\left[\int\limits_{-L / 2}^{0}\left(-x^{3}\right) d x+\int\limits_{0}^{+L / 2}\left(x^{3}\right) d x\right]$
$=16\left[-\left[\frac{x^{4}}{4}\right]_{-L / 2}^{0}+\left[\frac{x^{4}}{4}\right]_{0}^{+L / 2}\right]$
$=4\left[-\left[x^{4}\right]_{-L / 2}^{0}+\left[x^{4}\right]_{0}^{+L / 2}\right]$
$=4\left[-\left\{(0)^{4}-\left(-\frac{L}{2}\right)^{4}\right\}+\left\{\left(+\frac{L}{2}\right)^{4}-(0)^{4}\right\}\right]$
$=4\left[\left\{0-\frac{L^{4}}{16}\right\}+\left\{\frac{L^{4}}{16}-0\right\}\right]$
$=4\left[\frac{L^{4}}{16}+\frac{L^{4}}{16}\right]=4\left[\frac{L^{4}}{8}\right]=\frac{L^{4}}{2}$
Now by the theorem of parallel axes, the moment of inertia about axis $B B$, $I_{B B}=I_{C O M}+\int\left(\frac{L}{2}\right)^{2} d M=I_{C O M}+\frac{L^{2}}{4} \int d M$
Put the value of $d M$ and $I_{\text {com }}$
$I_{B B}=I_{M}+\frac{L^{2}}{4} \int\limits_{0}^{L / 2} \lambda |x| d x=\frac{L^{4}}{2}+\frac{L^{2}}{4} \lambda \int\limits_{0}^{L / 2}|x| d x$
$=\frac{L^{4}}{2}+\frac{L^{2}}{4} \times 16 \int\limits_{0}^{L / 2}(+x) d x$
$\left[\because \lambda=16\, kg / m ^{2}\right.$ (given) $]$
$=\frac{L^{4}}{2}+4 L^{2}\left[\frac{x^{2}}{2}\right]_{0}^{L / 2}=\frac{L^{4}}{2}+2 L^{2}\left[x^{2}\right]_{0}^{l / 2}$
$=\frac{L^{4}}{2}+2 L^{2}\left[\left(\frac{L}{2}\right)^{2}-(0)^{2}\right]$
$=\frac{L^{4}}{2}+2 L^{2}\left[\frac{L^{2}}{4}-0\right]$
$=\frac{L^{4}}{2}+\frac{L^{4}}{2}=L^{4}=1^{4}=1 kg - m ^{2}$