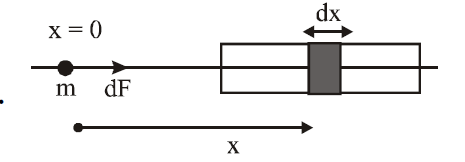
Q. A straight rod of length $L$ extends from $x = a$ to $x = L + a$. The gravitational force is exerts on a point mass $'m'$ at $x = 0$, if the mass per unit length of the rod is $A + Bx^2$, is given by:
Solution:
$dm =\left(A+Bx^{2}\right)dx$
$ dF = \frac{GMdm}{x^{2}} $
$ =F = \int^{a+L}_{a} \frac{GM}{x^{2}}\left(A +Bx^{2}\right)dx $
$ =GM \left[- \frac{A}{x}+Bx\right] ^{a+L}_{a} $
$ =GM\left[A \left(\frac{1}{a} -\frac{1}{a+L}\right) +BL \right]$