Q. A straight line $x-2 y-4=0$ is shifted parallel to it by 3 units away from the origin and then rotated by an angle of $30^{\circ}$ in the anti-clockwise direction. If the slope of the new line formed is $m$, then the intcgral part of ' $m$ ' is
TS EAMCET 2018
Solution:
$x-2y-4=0$
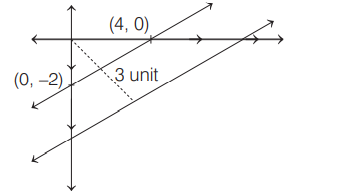
(i) Then rotates $30^{\circ}$ angle in only clockwise direction.
$\therefore $ slope of new line is $m$
(ii) Line is shifted 3 units away from origin. So, equation will be $x-2 y-7=0$
Now, it rotates $30^{\circ}$ angle in anticlockwise direction.
So,
x
y
x'
$cos\,\theta$
$sin\,\theta$
y'
$-sin\, \theta$
$cos\,\theta$
So, $x=x'\, \cos \,\theta-y'\, \sin \theta$
So, $y=x'\, \sin \theta+y'\, \cos \theta$
$x=\frac{x' \sqrt{3}}{2}-\frac{y'}{2}$ and $y=\frac{x'}{2}+\frac{\sqrt{3} y'}{2}$
Now, equation will be
$\left[\frac{\sqrt{3}}{2} x'-\frac{y'}{2}\right]-2\left[\frac{x'}{2}+\frac{\sqrt{3} y'}{2}\right]-7=0$
$\Rightarrow \, \left(\frac{\sqrt{3}-2}{2}\right) x'-\left(\frac{1+2 \sqrt{3}}{2}\right) y'=7$
So, $ m=\frac{\sqrt{3}-2}{1+2 \sqrt{3}} $
$\Rightarrow \,\frac{1.732-2}{1+2(1.732}$
So, integral part is (1)
| x | y | |
|---|---|---|
| x' | $cos\,\theta$ | $sin\,\theta$ |
| y' | $-sin\, \theta$ | $cos\,\theta$ |