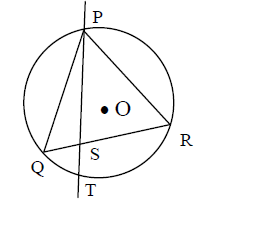
Question

A straight line through the vertex $P$ of a triangle PQR intersects the side $QR$ at the point $S$ and the circumcircle of the triangle PQR at the point $T$. If $S$ is not the centre of the circumcircle, then

• A. $\frac{1}{ PS }+\frac{1}{ ST } < \frac{2}{\sqrt{ QS \times SR }}$
• B. $\frac{1}{ PS }+\frac{1}{ ST } > \frac{2}{\sqrt{ QS \times SR }}$
• C. $\frac{1}{ PS }+\frac{1}{ ST } < \frac{4}{ QR }$
• D. $\frac{1}{ PS }+\frac{1}{ ST } > \frac{4}{ QR }$

Answer 1

Answer: (B), (D)

$PS \times ST = QS \times SR$
$\frac{\frac{1}{ PS }+\frac{1}{ ST }}{2}>\sqrt{\frac{1}{ PS } \times \frac{1}{ ST }}$
$\Rightarrow \frac{1}{ PS }+\frac{1}{ ST }>\frac{2}{\sqrt{ QS \times SR }}$
$\frac{ QS + SR }{2}>\sqrt{ QS \times SR }$
$\frac{ QR }{2}>\sqrt{ QS \times SR } $
$\Rightarrow \frac{1}{\sqrt{ QS \times SR }}>\frac{2}{ QR }$
$\Rightarrow \frac{1}{ PS }+\frac{1}{ ST }>\frac{4}{ QR }$