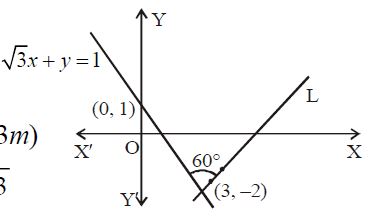Q. A straight line L through the point (3, -2) is inclined at an angle $60^°$ to the line $\sqrt{3}x+y=1$. If $L$ also intersects the x-axis, then the equation of L is
Straight Lines
Solution:
Let the slope of line L be $m$.
Then $\left|\frac{m+\sqrt{3}}{1-\sqrt{3}m}\right|=\sqrt{3}$
$\Rightarrow m+\sqrt{3}=\pm\left(\sqrt{3}-3m\right)$
$\Rightarrow 4m=0$ or $2m=2\sqrt{3}$
$\Rightarrow m=0$ or $m=\sqrt{3}$
$\because L$ intersects x-axis, $\,\therefore m=\sqrt{3}$
$\therefore $ Equation of $L$ is $y + 2 = \sqrt{3}\left(x-3\right)$
or $\sqrt{3}x-y-\left(2+x\sqrt{3}\right)=0$