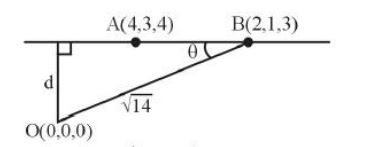
Question

A straight line $L$ intersects perpendicularly both the lines $\frac{x+2}{2}=\frac{y+6}{3}=\frac{z-34}{-10}$ and $\frac{x+6}{4}=\frac{y-7}{-3}=\frac{z-7}{-2}$ then the square of perpendicular distance of origin from $L$ is equal to

Answer 1

so $\|$ vector is $\overrightarrow{ b }=2 \hat{ i }+2 \hat{ j }+\hat{ k }$
Let line perpendicular to $L _1$ \& $L _2$ is $L$ with $A$ and $B$ points respectively on $L _1 \& L _2$
$A (2 \lambda-2,3 \lambda-6,-10 \lambda+34)$
$B (4 \mu-6,-3 \mu+7,-2 \mu+7)$
$A B$ is parallel to $2 \hat{i}+2 \hat{j}+\hat{k}$
$\therefore \frac{2 \lambda-4 \mu+4}{2}=\frac{3 \lambda+3 \mu-13}{2}=\frac{2 \mu-10 \lambda+27}{1}$
solving these,
$2 \lambda-4 \mu+4=3 \lambda+3 \mu-13 $
$\Rightarrow \lambda+7 \mu=17 \ldots(1)$
$\text { and } 3 \lambda+3 \mu-13=4 \mu-20 \lambda+54$
$\Rightarrow 23 \lambda-\mu=67 \ldots(2)$
and $3 \lambda+3 \mu-13=4 \mu-20 \lambda+54$
$\rightarrow 23 \lambda-\mu=67 \text {. }$
solving (1) and (2), $\lambda=3$ and $\mu=2$
$\therefore A \equiv(4,3,4) \text { and } B (2,1,3)$

$\cos \theta=\frac{\overrightarrow{ AB } \cdot \overrightarrow{ OB }}{|\overrightarrow{ AB }||\overrightarrow{ OB }|} $
$=\frac{4+2+3}{3 \cdot \sqrt{14}}=\frac{3}{\sqrt{14}} $
$d = OB \sin \theta=\sqrt{14} \cdot \frac{\sqrt{5}}{\sqrt{14}} \Rightarrow d =\sqrt{5} \Rightarrow d ^2=5$