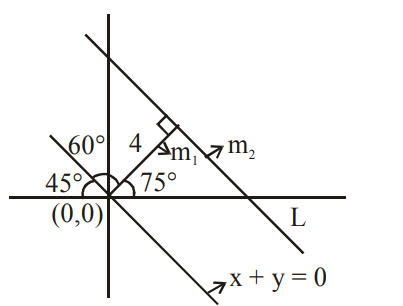Q. A straight line $L$ at a distance of $4$ units from the origin makes positive intercepts on the coordinate axes and the perpendicular from the origin to this line makes an angle of $60^\circ$ with the line $x + y = 0$. Then an equation of the line $L$ is :
Solution:
$m_1 = tan 75^{\circ} = \frac{\sqrt{3} + 1}{\sqrt{3} - 1}$
$m_2 = \frac{-1}{m_1} \, = \frac{-(\sqrt{3}-1)}{\sqrt{3}+1}$
$\Rightarrow \, \, y = m_2 x + C$
$\Rightarrow \, \, y \, = \frac{-(\sqrt{3}-1)x}{\sqrt{3}+1} + C \Rightarrow L$
Distance from origin = 4
$\therefore \, \, \, \frac{C}{\sqrt{1 + \frac{(\sqrt{3}-1)^2}{(\sqrt{3}+1)^2}}}$
$\Rightarrow \, \, \, \, \frac{(\sqrt{3} + 1)C}{\sqrt{8}} \, = 4$
$\Rightarrow \, \, C \, = \, \frac{8\sqrt{2}}{(\sqrt{3}+1)}$
Hence
$\Rightarrow \, \, \, (\sqrt{3}-1)y + (\sqrt{3} + 1 )x = 8\sqrt{2}$