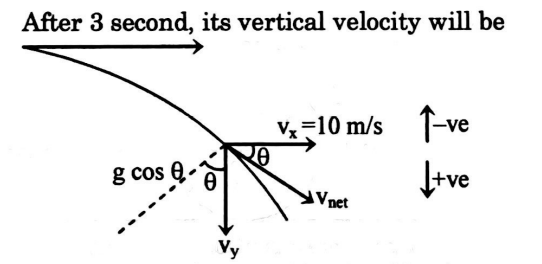
Q. A stone is thrown horizontally with a velocity $10\,m / s$. The radius of curvature of its trajectory in $3$ second after the motion began is $100 \sqrt{2 a}\, m$. Disregard the resistance of air. Determine $a$.
Laws of Motion
Solution: