Q.
A stone is projected from top of a vertical pole of height $3\, m$ with initial velocity $10 \,ms ^{-1}$. The maximum range on the ground is $\sqrt{10} x \,m$. The value of $x$ is ______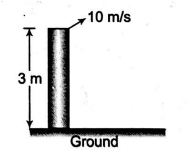
Motion in a Plane
Solution: