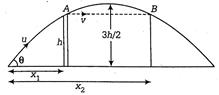
Q. A stone is projected from the point on the ground in such a direction so as to hit a bird on the top of a telegraph post of height and then attain the maximum height $ 3h/2 $ above the ground. If at the instant of projection, the bird were to fly away horizontally with uniform speed. Find the ratio between horizontal velocities of the bird and stone, if the stone still hits the bird while decreasing.
Jharkhand CECEJharkhand CECE 2015
Solution:
$ {{x}_{2}}=u\cos t\,\theta t,{{x}_{2}}-{{x}_{1}}=vt $
$ \Rightarrow $ $ {{x}_{1}}+vt=u\cos \theta t $
$ h=x\tan \theta -\frac{g{{x}^{2}}}{2{{u}^{2}}{{\cos }^{2}}\theta } $
$ \frac{3h}{2}=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g} $
Simplify to get, $ {{x}^{2}}-6h\,\cot \theta x+6{{h}^{2}}{{\cot }^{2}}\theta =0 $
$ x=\frac{6h\cot \theta \pm \sqrt{12}h\cot \theta }{2} $
$ =3h\cot \theta \pm \sqrt{3h}\cot \,\theta $
$ {{x}_{1}}=3h\cot \,\theta -\sqrt{3h}\cot \theta $ and
$ {{x}_{2}}=3h\cot \theta +\sqrt{3h}\cot \theta $
$ v=\frac{{{x}_{2}}-{{x}_{1}}}{t}=\frac{2\sqrt{3h}\cot \theta }{t} $
$ u\cos \theta =\frac{{{x}_{2}}}{t}=\frac{(3+\sqrt{3})h\cot \theta }{t} $
$ \frac{v}{u\cos \theta }=\frac{2\sqrt{3}}{3+\sqrt{3}}=\frac{2\sqrt{3}(3-\sqrt{3})}{9-3}=\sqrt{3}-1 $