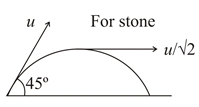
Question

A stone is projected at an angle $45^\circ $ with horizontal. A bee follows the trajectory of the stone at a constant speed equal to the initial speed of the stone. Neglect air resistance in motion of stone. The magnitude of acceleration (in $ms^{- 2}$ ) of the bee at the topmost point of its trajectory is $9.8\alpha .$ Write the value of $\alpha .$
$\left(\right.g= 9 . 8\, m s^{- 2}$

Answer 1

Let initial velocity of the stone be $u$
For stone, at the highest point Radius of curvature, $R=\frac{\left(u / \sqrt{2}\right)^{2}}{ g}=\frac{u^{2}}{2 g}$
The bee follows the stone's trajectory with the constant speed $u$ , $a=\frac{u^{2}}{R}=\frac{u^{2}}{u^{2} / 2 g}=2g$
$a=2g=19.6\, ms^{- 2}=2\times 9.8$