Question

A stiff metal rod is kept over two knife edges of length $L=1 \,m$ as shown in the figure.

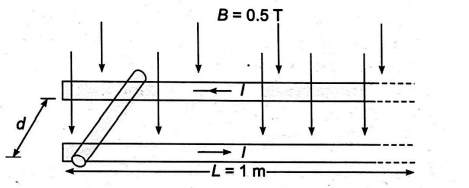
The rod carries a current of $16 \,A$ (in the direction shown) and rolls along the rails without slipping due to the magnetic force produced by a uniform magnetic field of $0.5\, T$ perpendicular and pointing downwards. If rod starts from rest and its speed when it leaves the rails is $\frac{k}{\sqrt{5}} \,ms ^{-1}$, then the value of $k$ is _______

Answer 1

Force on rod, $F=I(d \times B)=I d B(\hat{i})$
By work-energy theorem
$KE ($ Translation $)+ KE ($ Rotation $)=$ Work done
$\Rightarrow F \times L=\frac{1}{2} m v^{2}+\frac{1}{2}\left(I \omega^{2}\right) $
$\Rightarrow I d B L=\frac{1}{2} m v^{2}+\frac{1}{2}\left(\frac{1}{2} m R^{2}\right)\left(\frac{v}{R}\right)^{2} $
$\Rightarrow I d B L=\frac{3}{4} m v^{2} $
Or $ v=\left(\frac{4 I d B L}{3 m}\right)$
$=\sqrt{\frac{4 \times 16 \times\left(10 \times 10^{-2}\right) \times 0.5 \times 1}{\left(3 \times \frac{1}{3}\right)}}$
$=\sqrt{64 \times \frac{1}{2} \times 10^{-1}}=4 \times \frac{1}{\sqrt{5}} ms ^{-1}$