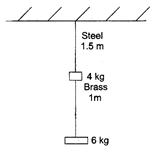
Q.
A steel wire of $1.5\, m$ long of diameter $0.25\, cm$ and a brass wire of $1.0\,m$ long of diameter $0.25\,m$ are loaded as shown. Calculate, the elongation of the brass wire.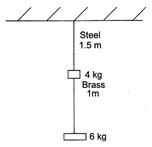
AMUAMU 2014Mechanical Properties of Solids
Solution:
If a wire of length $L$ and radius $r$ increase in length by $\Delta L$ under
a suspended load $Mg$,
then the Youngs modulus of the material of the wire is
$Y=\frac{M g L}{\left(\pi r^{2}\right) \times \Delta L}$
or $\Delta L=\frac{M g L}{\left(\pi r^{2}\right) Y}$
For the brass wire, the suspended load is
$6.0\, kg \times 9.8 \,N / kg$
$=58.8 N$
$\therefore $ Elongation of the brass wire is given by
$\Delta L_{\text {Brass }}=\frac{(M g)_{B r} \times L_{B r}}{\left(\pi r^{2}\right) \times Y_{B r}}$
$=\frac{58.8 \times 1.0}{3.14 \times\left(0.125 \times 10^{-2}\right)^{2} \times 0.91 \times 10^{11}}$
$=13 \times 10^{-4}\, m$