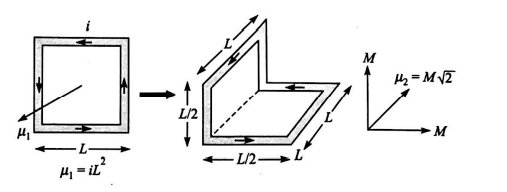
Question

A steady current $i$ flows in a small square loop of wire of side $L$ in a horizontal plane. The loop is now folded about its middle such that half of it lies in a vertical plane. Let $\overrightarrow{\mu_{1}}$ and $\overrightarrow{\mu_{2}}$ respectively denote the magnetic moments due to the current loop before and after folding. Then

• A. $\overrightarrow{\mu_{2}}=0$
• B. $\overrightarrow{\mu_{1}}$ and $\overrightarrow{\mu_{2}}$ are in the same direction
• C. $\frac{\left|\overrightarrow{\mu_{1}}\right|}{\left|\overrightarrow{\mu_{2}}\right|}=\sqrt{2}$
• D. $\frac{\left|\overrightarrow{\mu_{1}}\right|}{\left|\overrightarrow{\mu_{2}}\right|}=\left(\frac{1}{\sqrt{2}}\right)$

Answer 1

Answer: (C)

Initial magnetic moment $=\mu_{1}=i L^{2}$
After folding the loop, $M=$ magnetic moment due to each
part $=i\left(\frac{L}{2}\right) \times L=\frac{i L^{2}}{2}=\frac{\mu_{1}}{2}$
$\Rightarrow \mu_{2}=M \sqrt{2}=\frac{\mu_{1}}{2} \times \sqrt{2}=\frac{\mu_{1}}{\sqrt{2}} $
or $ \frac{\mu_{1}}{\mu_{2}}=\sqrt{2}$