Q.
A square wire loop with side $L=1.0\, m$ sides is perpendicular to a uniform magnetic field, with half the area of the loop in the field as shown in figure. The resistance of the loop is $35\, \Omega$ and the loop contains an ideal battery with emf $\varepsilon=6.0\, V$. If the magnitude of the field varies with time according to $B=5.0-2.0\, t$, with $B$ in tesla and $t$ in seconds, what is current (in $A$) around the loop?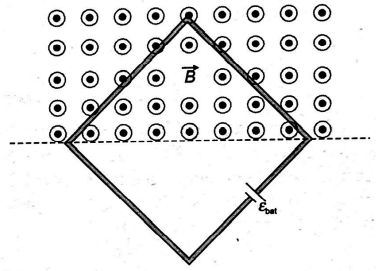
Electromagnetic Induction
Solution: