Question

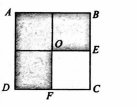
A square of side $4\, cm$ and of uniform thickness is divided into four equal squares. If one of them is cut off $(OECF)$, then the position of the centre of mass of the remaining portion from $O$ is

• A. $\frac{1}{\sqrt{3}}\, cm$
• B. $\frac{2}{\sqrt{3}} \,cm$
• C. $\frac{5}{\sqrt{3}} \,cm$
• D. $\frac{\sqrt{2}}{3} \,cm$

Answer 1

Answer: (D)

$W$ = Whole square $ABCD$
$C=$ Cut square $OECF$
$R=$ Remaining part of square i.e. shaded region.
Now center of mass of the whole square is at $O(0,0)$.
The $CM$ of cut square is at its centre namely $(1 \,cm ,-1 \,cm )$ Let mass per unit area $=\sigma$
$x_{W}=\frac{m_{C} x_{C}+m_{R} m_{R}}{m_{C}+m_{R}}$
$0=\frac{\sigma\left(12 cm ^{2}\right) \cdot x_{R}+\sigma\left(4 cm ^{2}\right) \cdot(1 cm )}{\sigma\left(16 \,cm ^{2}\right)}$

$\Rightarrow x_{R}=-\frac{1}{3} \,cm$
Similarly, $y_{W}=\frac{m_{C} y_{C}+m_{R} y_{R}}{m_{C}+m_{R}}$
$0=\frac{\sigma\left(12 cm ^{2}\right) \cdot\left(y_{R}\right)+\sigma\left(4 cm ^{2}\right) \cdot(-1 cm )}{\sigma\left(16 cm ^{2}\right)}$
$\Rightarrow y_{R}=\frac{1}{3}\, cm$
Distance from origin of $\left(x_{R}, y_{R}\right)$
$=\sqrt{x_{R}^{2}+y_{R}^{2}}=\sqrt{\left(\frac{1}{3}\right)^{2}+\left(\frac{1}{3}\right)^{2}}$
$=\frac{\sqrt{2}}{3} \,cm$