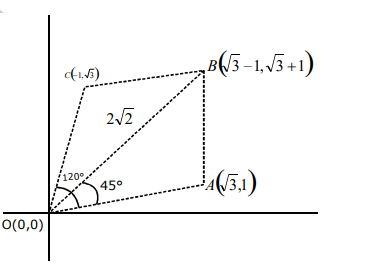
Question

A square, of each side $2$, lies above the $x-axis$ and has one vertex at the origin. If one of the sides passing through the origin makes an angle $30^{\circ}$ with the positive direction of the $x$-axis, then the sum of the $x$-coordinates of the vertices of the square is :

• A. $2 \sqrt{3} - 1 $
• B. $2 \sqrt{3} - 2 $
• C. $ \sqrt{3} - 2 $
• D. $ \sqrt{3} - 1 $

Answer 1

Answer: (B)

$\frac{x}{\cos 30^{\circ}}=\frac{y}{\sin 30^{\circ}}=2$
$x=\frac{2 \sqrt{3}}{2}=\sqrt{3}$
$y=1$
$\frac{x}{\cos 120^{\circ}}=\frac{y}{\sin 120^{\circ}}=2$
$x=-1, y=\sqrt{3}$
$\frac{x}{\cos 75^{\circ}}=\frac{y}{\sin 75^{\circ}}=2 \sqrt{2}$
$x=\sqrt{3}-1$
$y=\sqrt{3}+1$
sum $=0+\sqrt{3}+\sqrt{3}-1+(-1)$
$=2 \sqrt{3}-2$