Q.
A square metal wire loop $P Q R S$ of side $10\, cm$ and resistance $1 \Omega$ is moved with a constant velocity $v$ in a uniform magnetic field of $B=2\, Wb\, m ^{-2}$, as shown in the figure. The magnetic field lines are perpendicular to the plane of the loop (directed into the paper). The loop is connected to network $A B C D$ of resistors each of value $3\, \Omega .$ The resistance of the lead wires $S B$ and $R D$ are negligible. The speed of the loop so as to have a steady current of $1\, mA$ in the loop is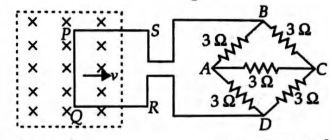
Electromagnetic Induction
Solution: