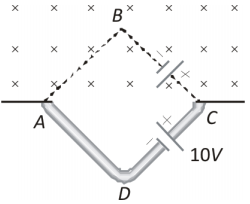
Q.
A square loop of side $1m$ is placed in a perpendicular magnetic field. Half of the area of the loop inside the magnetic field. A battery of emf $10V$ and negligible internal resistance is connected in the loop. The magnetic field changes with time according to relation $B=\left(0 . 01 - 2 t\right)Tesla$ . The resultant emf in the loop will be
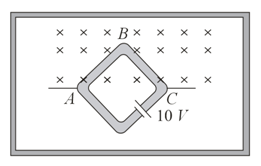
NTA AbhyasNTA Abhyas 2020
Solution: