Question

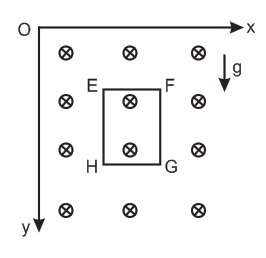
A square loop $EFGH$ of side $a$ , mass $m$ and total resistance $R$ is falling under gravity in a region of transverse non-uniform magnetic field given by $B=B_{0}\frac{y}{a}$ , where $B_{0}$ is a positive constant and $y$ is the position of side $EF$ of the loop. If at some instant the speed of the loop is $v$ , then the total Lorentz force acting on the loop is

• A. $F=\frac{B_{0}^{2} a^{2} v}{2 R}$
• B. $F=\frac{2 B_{0}^{2} a^{2} v}{R}$
• C. $F=\frac{B_{0}^{2} a^{2} v}{R}$
• D. zero

Answer 1

Answer: (C)

Motional emf in EH and FG = 0 as $\overset{ \rightarrow }{\text{v}} \left||\right. \overset{ \rightarrow }{\text{I}}$
Motional emf in EF is $e_{1}=\left(\frac{\left(\text{B}\right)_{0} \text{y}}{\text{a}}\right)\left(\text{a}\right)v =\left(\text{B}\right)_{0}\text{y}v⁡$
Similarly, motional emf in GH will be
$\left(\text{e}\right)_{2}=\left\{\frac{\left(\text{B}\right)_{0} \left(\text{y} + \text{a}\right)}{\text{a}}\right\}\left(\text{a}\right)\left(v \right)=\left(\text{B}\right)_{0}\left(\text{y} + \text{a}\right)v⁡$
Polarities of e₁and e₂ are shown in adjoining figures.

So the net emf is
$e=e_{2}-e_{1}e=B_{0}av$
$\text{i} = \frac{\text{e}}{\text{R}} = \frac{\text{B}_{0} \text{a} v }{\text{R}}$

$\left(\text{F}\right)_{\text{EF}} = \left(\frac{{B}_{0} {a} v }{\text{R}}\right) \left(\text{a}\right) \left(\frac{{B}_{0} \text{y}}{\text{a}}\right)$ (downwards)
$\left(\text{F}\right)_{\text{GH}} = \left(\frac{\left(\text{B}\right)_{0} \text{a} v }{\text{R}}\right) \left(\text{a}\right) \left(\frac{\left(\text{B}\right)_{0} \left(\text{y} + \text{a}\right)}{\text{a}}\right)$
$\left(\text{F}\right)_{\text{GH}}=\left(\frac{\text{B}_{0}^{2} \text{a} v }{\text{R}}\right)\left(\text{y} + \text{a}\right)$ (upwards)
Net Lorentz force on the loop
$F_{net}=\text{F}_{\text{GH}}-\text{F}_{\text{EF}}=\frac{\text{B}_{0}^{2} \text{a}^{2} v }{\text{R}}$
$F=\frac{B_{0}^{2} a^{2} v}{R}$