Q.
A square hole of side length $l$ is made at a depth of $h$ and a circular hole of radius $r$ is made at a depth of $4h$ from the surface of water in a water tank kept on a horizontal surface. If $ \ell<< h, r<< h$ and the rate of water flow from the holes is the same, then $r$ is equal to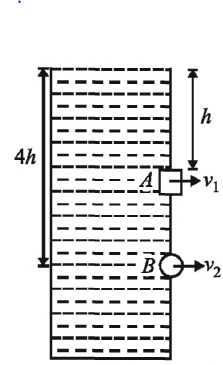
AIEEEAIEEE 2012Mechanical Properties of Fluids
Solution: