Question

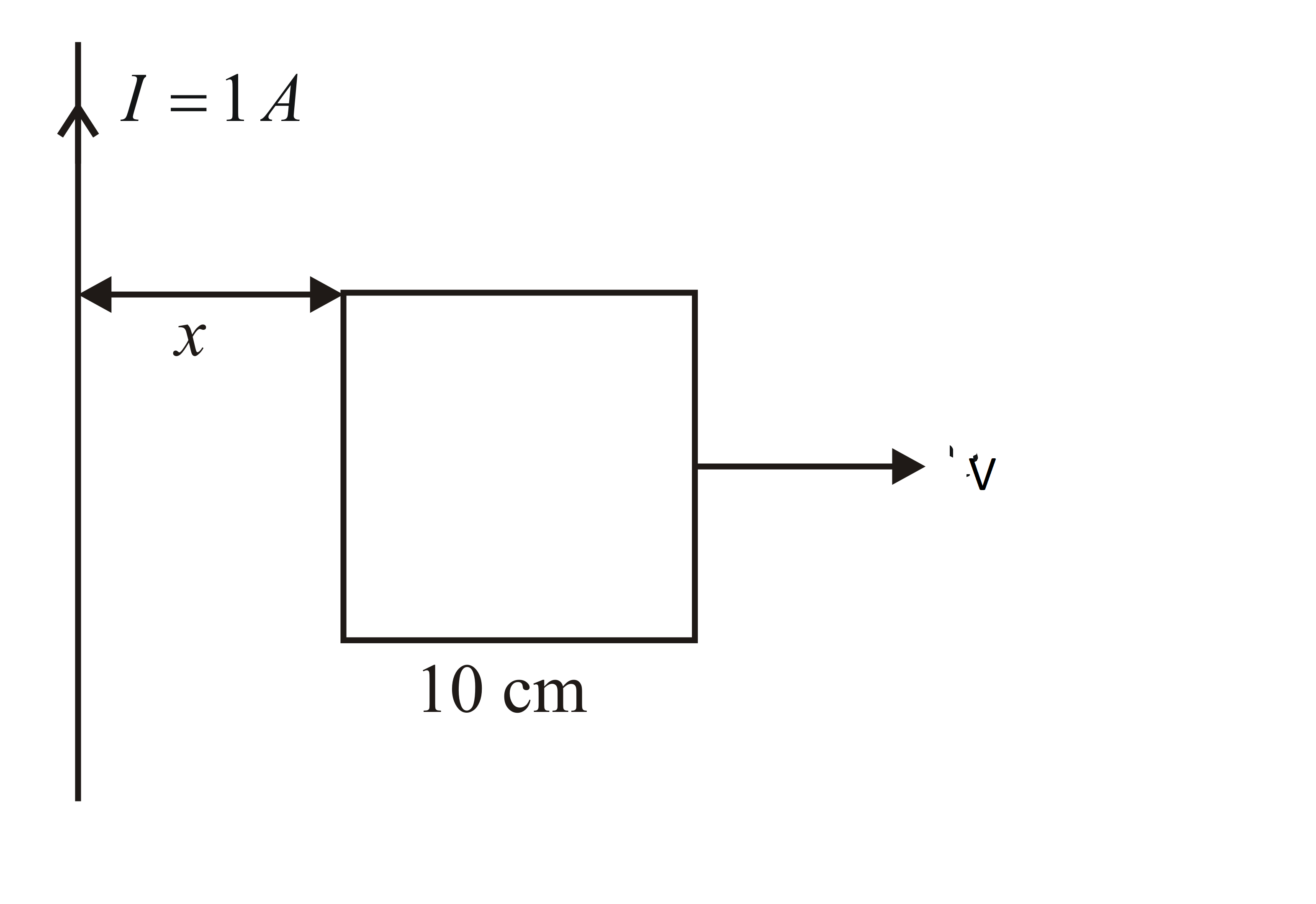
A square frame of side $10cm$ and a long straight wire carrying current $1A$ are in the plane of the paper. Starting from close to the wire, the frame moves towards the right with a constant speed of $10ms^{- 1}$ (see figure). The e.m.f induced at the time the left arm of the frame is at $x=10cm$ from the wire is

• A. $0.75μV$
• B. $1μV$
• C. $2μV$
• D. $0.5μV$

Answer 1

Answer: (B)

$d\phi=\frac{\mu _{0} i}{2 \pi y}ady$
$\phi=\frac{\left(\mu \right)_{0} i a}{2 \pi }\displaystyle \int _{x}^{x + a}\frac{d y}{y}=\frac{\left(\mu \right)_{0} i a}{2 \pi }\left[l n \left(x + a\right) - l n x\right]$
$\text{E.m.f}=-\frac{d \phi}{d t}=-\frac{\mu _{0} i a}{2 \pi }\left[\frac{1}{x + a} \frac{d x}{d t} - \frac{1}{x} \frac{d x}{d t}\right]$
$=\frac{\left(\mu \right)_{0} i a}{2 \pi }\frac{a . v}{x \left(x + a\right)}=\frac{\left(\mu \right)_{0}}{2 \pi }.\frac{i a^{2} v}{x \left(x + a\right)}=2\times \left(10\right)^{- 7}\times \frac{1 \times \left(\left(0.1\right)^{2} \times 10\right)}{0.1 \times 0.2}=1\mu V$
Alternative method:
Consider two sides which are perpendicular to the velocity as case of motional e.m.f.

$E=E_{1}-E_{2}=\left(B_{1} - B_{2}\right)Vl$
$=\frac{\left(\mu \right)_{0} I}{2 \pi }\left(\frac{1}{x} - \frac{1}{x + a}\right)Vl$
$=2\times \left(10\right)^{- 7}\times 1\left(\frac{1}{0.1} - \frac{1}{0.2}\right)\times 10\times 0.1$
$=10^{- 6}V=1μV$