Question

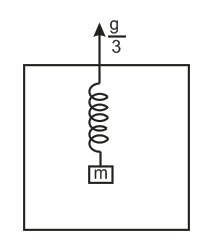
A spring of spring constant $200 \, N \, m^{- 1}$ has a block of mass $1 \, kg$ hanging at its one end and from another end, spring is attached to a ceiling of an elevator. The elevator rising upwards with an acceleration of $g/3$ . When acceleration suddenly ceases, then angular velocity and elongation during the time when the elevator is accelerating

• A. $14.14rads^{- 1},0.07m$
• B. $13 \, rad \, s^{- 1}, \, 0.1 \, m$
• C. $14 \, rad \, s^{- 1}, \, 0.05 \, m$
• D. $10 \, rad \, s^{- 1}, \, 0.07 \, m$

Answer 1

Answer: (A)

The angular frequency under all circumstances is
$\omega = \sqrt{\left(\frac{\text{k}}{\text{m}}\right)}$
$= \sqrt{\left(\frac{2 0 0}{1}\right)} = 1 4 \text{.} 1 4 \text{ rad} / \text{s}$

When elevator is moving up, using NLM
$\text{T} - \text{mg} = \frac{\text{mg}}{3} \Rightarrow \text{T} = \frac{4 \text{mg}}{3}$
This tension elongates the spring by x
$\text{T} = \text{kx} \, \, ⇒ \, \, \text{x} = \frac{4 \text{mg}}{3 \text{k}} = 0 \text{.} 0 7 \text{ m}$