Q.
A spring is compressed between two blocks of masses $m_1$ and $m_2$ placed on a horizontal frictionless surface as shown in the figure. When the blocks are released, they have initial velocity of $v_1$ and $v_2$ as shown. The blocks travel distances $x_1$ and $x_2$ respectively before coming to rest. The ratio $\left(\frac{x_{1}}{x_{2}}\right)$ is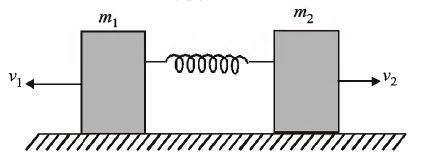
AIEEEAIEEE 2012Laws of Motion
Solution: