Question

A spout pipe of diameter $0.5\, cm$ is connected horizontally at the bottom of a cylindrical vessel of diameter $15\, cm$ as shown in figure below.

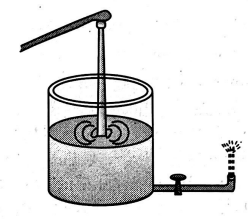
When water is poured into the vessel, it leaves the spout in the form of a fountain. Find the height (in $m$ ) to which the vertical stream of water goes, if the water level in the vessel is maintained at a constant height of $0.45\, m$. (Take $g=10\, m / s ^{2}$ )

Answer 1

Depth of spout pipe, $h =0.45\, m$;
$\therefore $ Velocity of efflux through the spout pipe,
$v =\sqrt{2 gh }=\sqrt{2 \times 10 \times 0.45}=3\, ms ^{-1}$
According to Bernoulli's theorem,
$\frac{P}{\rho}+g h+\frac{1}{2} v^{2}=$ constant
At the mouth of the spout pipe and the top of fountain, pressure is same (equal to atmospheric pressure).
$\therefore gh +\frac{1}{2} v ^{2}=$ constant
At the mouth of the spout pipe, $h =0$ and $v =3\, ms ^{-1}$
Also, at the top of fountain, $v=0$
Suppose that stream of water in the form of fountain goes up to a height $h '$. Then,
$10 \times h'+\frac{1}{2} \times(0)^{2}=10 \times 0+\frac{1}{2} \times(3)^{2}$
$\therefore h '=\frac{1}{2} \times \frac{9}{10}=0.45 m$