Q.
A spherically symmetric charge distribution is considered with charge density varying as $\rho(r)= \begin{cases}\rho_0\left(\frac{3}{4}-\frac{r}{R}\right) & \text { for } r \leq R \\ \text { Zero } & \text { for } r>R\end{cases}$
Where, $r ( r < R )$ is the distance from the centre $O$ (as shown in figure). The electric field at point $P$ will be :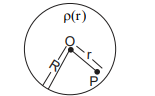
Solution:
