1. Tardigrade
  2. Question
  3. Physics
  4. A spherical surface of radius of curvature R, separates air (refractive index 1.0) from glass (refractive index 1.5). The centre of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The line PQ cuts the surface at a point O and PO = OQ. The distance PO is equal to

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

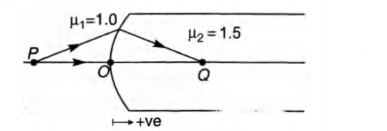
Q. A spherical surface of radius of curvature R, separates air (refractive index 1.0) from glass (refractive index 1.5). The centre of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The line PQ cuts the surface at a point O and PO = OQ. The distance PO is equal to

IIT JEEIIT JEE 1998

Solution:

Let us say PO = OQ = X
Applying$\, \, \, \, \, \, \, \, \frac{\mu_2}{v}-\frac{\mu_1}{u}=\frac{\mu_1-\mu_2}{R}$
Substituting the values with sign
$\frac{1.5}{+X}-\frac{1.0}{-X}=\frac{1.5-1.0}{+R}$
(Distances are measured from O and are taken as positive in
the direction of ray of light)
$\therefore \frac{2.5}{X}=\frac{0.5}{R}$
$\therefore X=5R$

Solution Image