Q.
A spherical rigid ball is released from rest and starts rolling down an inclined plane from height $h\, =\, 7\,m$, as shown in the figure. It hits a block at rest on the horizontal plane (assume elastic collision). If the mass of both the ball and the block is m and the ball is rolling without sliding, then the speed of the block after collision is close to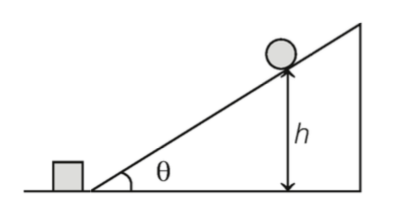
KVPYKVPY 2019System of Particles and Rotational Motion
Solution:
