Question

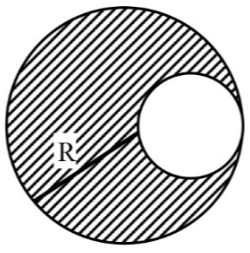
A spherical hole is made in a solid sphere of radius $R$ . The mass of the sphere before hollowing was $M$ . The gravitational field at the centre of the hole due to the remaining mass is -

• A. zero
• B. $\frac{G M}{8 R^{2}}$
• C. $\frac{G M}{2 R^{2}}$
• D. $\frac{G M}{R^{2}}$

Answer 1

Answer: (C)

By the principle of superposition of fields
$\overset{ \rightarrow }{E}=\overset{ \rightarrow }{E_{1}}+\overset{ \rightarrow }{E_{2}}$
Here, $\overset{ \rightarrow }{E}=net \, field \, at \, the \, centre \, of \, hole \, due \, to \, entire \, mass$
$\overset{ \rightarrow }{E_{1}}=field \, due \, to \, remaining \, mass$
and $\overset{ \rightarrow }{E_{2}}=field \, due \, to \, mass \, in \, hole=0$
$\therefore \overset{ \rightarrow }{E_{1}}=\overset{ \rightarrow }{E}=\left(\frac{G M}{R^{3}}\right).r$
where $r=\frac{R}{2}$
$\therefore \, \overset{ \rightarrow }{E}=\frac{G M}{2 R^{2}}$