Question

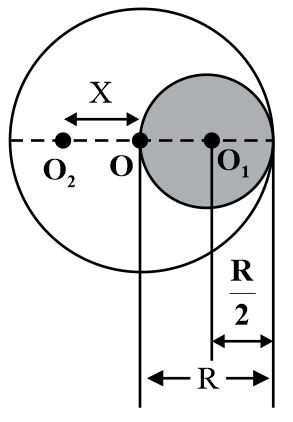
A spherical cavity is made in a lead sphere of radius $R$ such that its surface touches the outside surface of lead sphere and passes through the centre. The shift in the centre of mass of the lead sphere as a result of this hollowing, is

• A. $\frac{\text{R}}{7}$
• B. $\frac{\text{R}}{14}$
• C. $\frac{\text{R}}{2}$
• D. R

Answer 1

Answer: (B)

Let centre of mass of lead sphere after hollowing be at point $O_{2}$ , where $OO_{2}=x$
Mass of spherical hollow $m=\frac{\frac{4}{3} \pi \left(\frac{\text{R}}{2}\right)^{2} \text{M}}{\left(\frac{4}{2} \pi \left(\text{R}\right)^{3}\right)}=\frac{\text{M}}{8}$ and
$\text{x}=\text{OO}_{1}=\frac{\text{R}}{2}$

$\therefore \text{x}=\frac{\text{M} \times 0 - \left(\frac{\text{M}}{8}\right) \times \frac{\text{R}}{2}}{\text{M} - \frac{\text{M}}{8}}=\frac{\frac{\text{MR}}{16}}{\frac{7 \text{M}}{8}}=-\frac{\text{R}}{14}$
$\therefore \text{shift} = \frac{\text{R}}{1 4}$