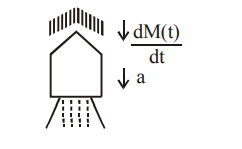
Q. A spaceship in space sweeps stationary interplanetary dust. As a result, its mass increases at a rate $\frac{ dM ( t )}{ dt }= bv ^{2}( t ),$ where $v ( t )$ is its instantaneous velocity. The instantaneous acceleration of the satellite is:
Solution: