Question

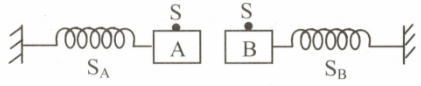
A source s emitting sound of $400\,Hz$ is fixed on block A which is attached to free end of a spring $S_{A}.$ The detector $D$ fixed on block $B$ attached to the free end of spring $S_{B}$ detects this sound. The blocks A and B are simultaneously displaced towards each other through a distance of $1.0\,m$ and then left to vibrate. If vibrational frequency of each block is $3\,Hz,$ the maximum frequencies of sound detected by D is $nhz$ . Then, what is the value of $n$ ?
$\left(v_{\text{sound }} = 340\, m / s\right)$

Answer 1

$\omega =2\pi v=2\pi \left(\right.3\left.\right)=6\pi $
$\therefore \omega =18.85rads^{- 1}$
Maximum speed of motion of $\left|v_{A}\right|$ and $\left|v_{B}\right|=A\omega $
$f_{max}=\left(\frac{v + v_{B}}{v - v_{A}}\right)f=\left(\frac{340 + A \omega }{340 - A \omega }\right)f$
$=\left(\frac{340 + 18 . 85}{340 - 18 . 85}\right)400$
$=\left(\frac{358 . 85}{321 . 15}\right)\times 400$
$=1.12\times 400$
$\therefore f_{max}=448\,Hz$