Q.
A solid spherical region having a spherical cavity whose diameter $R$ is equal to the radius of the spherical region, has a total charge $Q$. The electric field at a point $P$ as shown is $\frac{Q}{28 \pi \varepsilon_{0}}\left[\frac{A}{x^{2}}-\frac{B}{\left(x-\frac{R}{2}\right)^{2}}\right]$. Find $(A-B)$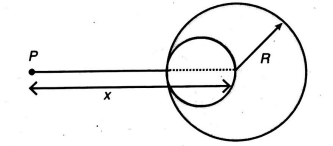
Electric Charges and Fields
Solution:
