Question

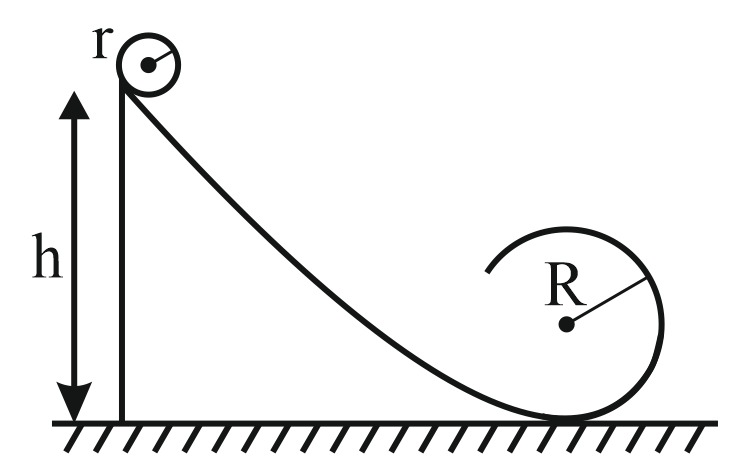
A solid sphere rolls without slipping along the track shown in the figure. The sphere starts from rest from a height $h$ above the bottom of the loop of radius $R$ which is much larger than the radius of the sphere $r$ . The minimum value of $h$ for the sphere to complete the loop is

• A. 2.1 R
• B. 2.3 R
• C. 2.7 R
• D. 2.5 R

Answer 1

Answer: (C)

At the topmost point of the loop minimum value of the linear speed of the centre of the sphere should be : $v=\sqrt{g R}$
or translational kinetic energy
$K_{ T }=\frac{1}{2} m v^{2}=\frac{1}{2} m g R$.
In case of pure rolling of a solid sphere the ratio of rotational to translational kinetic energy is : $\frac{K_{ R }}{K_{ T }}=\frac{2}{5}$
$\therefore$ Total kinetic energy at topmost point should be :
$K=\frac{5+2}{5} \cdot(K)_{ T }=\frac{7}{5}\left(\frac{1}{2} m g R\right)=\frac{7}{10} m g R$
Now from conservation of mechanical energy:
$\frac{7}{10} m g R=m g(h-2 R)$
$\therefore h=2.7 R$