Question

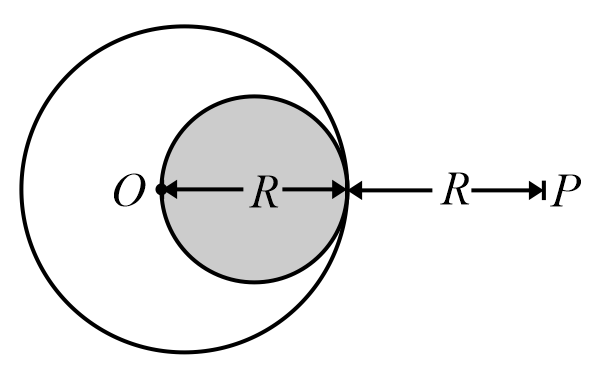
A solid sphere of uniform density and radius $r$ applies a gravitational force of attraction equal to $F_{1}$ on a particle placed at $P$ , at a distance $2R$ from the centre $O$ of the sphere. A spherical cavity of the radius $\frac{R}{2}$ is now made in the sphere as shown in the figure. The sphere with cavity now applies a gravitational force $F_{2}$ on the same particle placed at $P$ . The ratio $\frac{F_{2}}{F_{1}}$ will be,

• A. $\frac{1}{2}$
• B. $\frac{7}{9}$
• C. $3$
• D. $7$

Answer 1

Answer: (B)

Gravitational force due to solid sphere, $F _{1} = \frac{G ⁡ M ⁡ m ⁡}{\left(2 R ⁡\right)^{2}} \text{,}$
where $M$ and $m$ are mass of the solid sphere and particle respectively and $R$ is the radius of the sphere. The gravitational force on particle due to sphere with cavity = force due to solid sphere creating cavity, assumed to be present above at that position
i.e., $F_{2}=\frac{G M m}{4R^{2}}=\frac{G(M / 8) m}{(3 R / 2)^{2}}=\frac{7}{36} \frac{G M m}{R^{2}}$
So, $\frac{F_{2}}{F_{1}}=\frac{7 G M m}{36R^{2}} /\left(\frac{G M m}{4R^{2}}\right)=\frac{7}{9}$